SP3

ODE-based modeling of drug response in HER2-low breast cancer

Key question of the subproject is the identification and quantitative description of the mechanisms of action of different targeted therapeutics employed to treat breast cancer with low to moderate expression levels of HER2 (ERBB2). To this end, biologically motivated mathematical models of the cell are designed to describe the interactions of receptors and signaling pathway proteins.
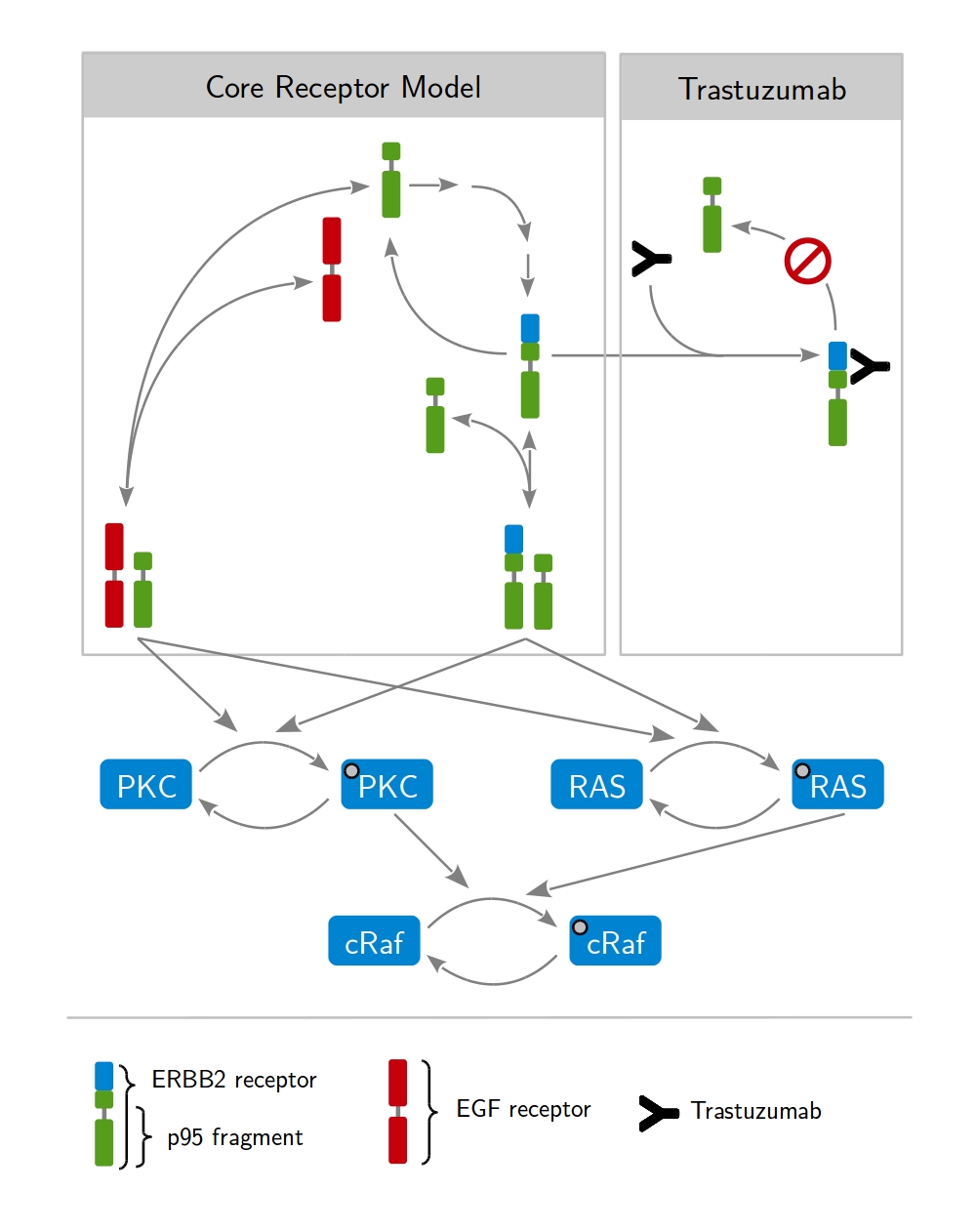
Our approach is based on dynamic modeling. A dynamic model describes the time evolution of a biological systems by differential equations. Those express loss and gain of the modeled protein concentrations. The formation of receptor dimers and the subsequent phosphorylation of intracellular proteins present fundamental processes, as shown in Fig. 1. Considering all possible interactions leads to a huge network of coupled differential equations. A key aspect of modeling is therefore the identification of biologica processes that are relevant for the given problem and and need to be included in the model. Fig. 2 shows a model describing the mechanism of action of the therapeutic antibody trastuzumab clinically applied to treat HER2-high breast cancer.

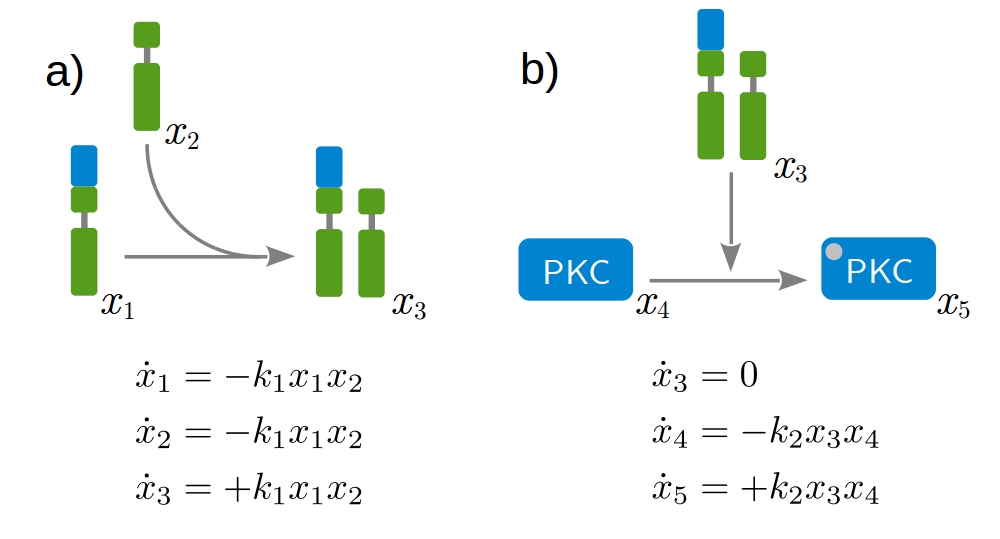
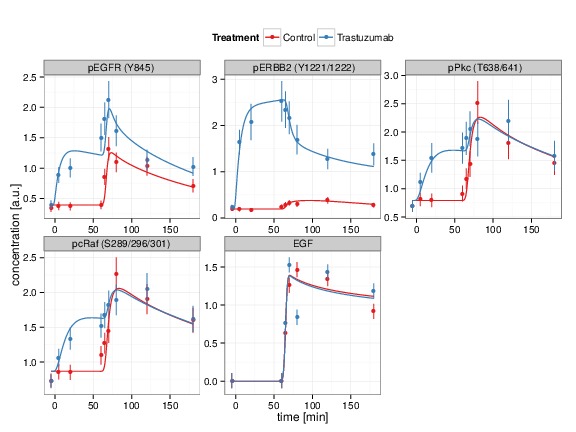
Fig. 1: Fundamental interactions. a) The formation of a dimer x3 is proportional to the concentrations of the participating receptors x1 and x2. The concentrations of the monomeric receptors are thereby reduced by the corresponding quantity. b) Receptor dimers can further activate intracellular proteins. The transformation of the non-phosphorylated protein x4 into the phosphorylated protein x5 depends on the concentration of the x3 dimers.

Fig. 2: Model for the interactions of ERBB2 and EGFR and the activation of PKC, RAS and cRAF proteins in HER2-high breast cancer cells. Trastuzumab binds to the extracellular domain of ERBB2 and inhibits its cleavage.

The interaction terms contain reaction rates which are frequently unknown and need to be estimated from experimental data. The necessary data for this procedure are time-resolved measurements of protein concentrations as being provided by our experimental project partners. To determine those parameter values that give rise to an optimal fit between data and model prediction, an objective function is defined, the so-called log-likelihood. This function provides a measure for the concordance between model prediction and experimental data in such a way that the most likely parameter values are those that maximize the objective function. The parameter fit also allows to assess if the model is able to describe the data at all, like shown in Fig. 3, or if changes of the model are required.
In the frame of this project, established dynamic breast cancer models are extended to describe the mechanisms of action of additional drugs in various breast cancer cell lines. The insights gained in these systems help to formulate new strategies for optimizing the efficacy of breast cancer drugs.